[알고리즘] Backtracking

> Backtracking

- Recursive하게 문제를 해결하는 방법

- Problem space는 각 state(node)들과 action들로 구성

 

*possible goals of backtracking

-> success를 위한 하나의 패스 찾기

-> success를 위한 모든 패스 찾기

-> success를 위한 가장 좋은 패스 찾기

 

BACKTRACKING(u)
	if at a solution: return success
    	for each child v of u :
    		if promising(v) :	//u의 자식노드 subproblem v가 promising한지 판별
        		result <- BACKTRACKING(v)
            		if result ≠ failure: return result
	return failure

 

우리는 Backtracking 중 N Queens problem에 대해 자세히 알아볼 것이다.

 

> N-Queens Problem

- n x n 체스보드

- 서로서로 공격당할 수 없는 위치에 놓아야 함

- 4 x 4 체스보드에서는 총 16 * 15 * 14 * 13 = 43,680가지의 case가 존재

-> search space를 줄여야 함!

 

sketch idea :

1) 첫 번째 Queen을 임의로 둔다.

2) 그 다음 Queen을 safe places에 둔다.

3) 이 과정을 반복한다.

   > 위치에 둬야 할 queen이 더 이상 없을 경우(모든 queen이 자리잡을 때까지)

   > no safe place is left (safe place가 더 이상 없을 경우)

4) 이때, 3번의 과정에서 no safe place is left일 경우, 그 이전의 자리를 둔 queen의 자리를 다시 바꾼다.

=> 4번의 과정이 바로 backtracking!

 

*row별로 계산 -> 4 * 4 * 4 * 4 = 256 ways 존재

 

=> recursion tree를 통해서 backtracking algorithm의 실행을 확인 가능

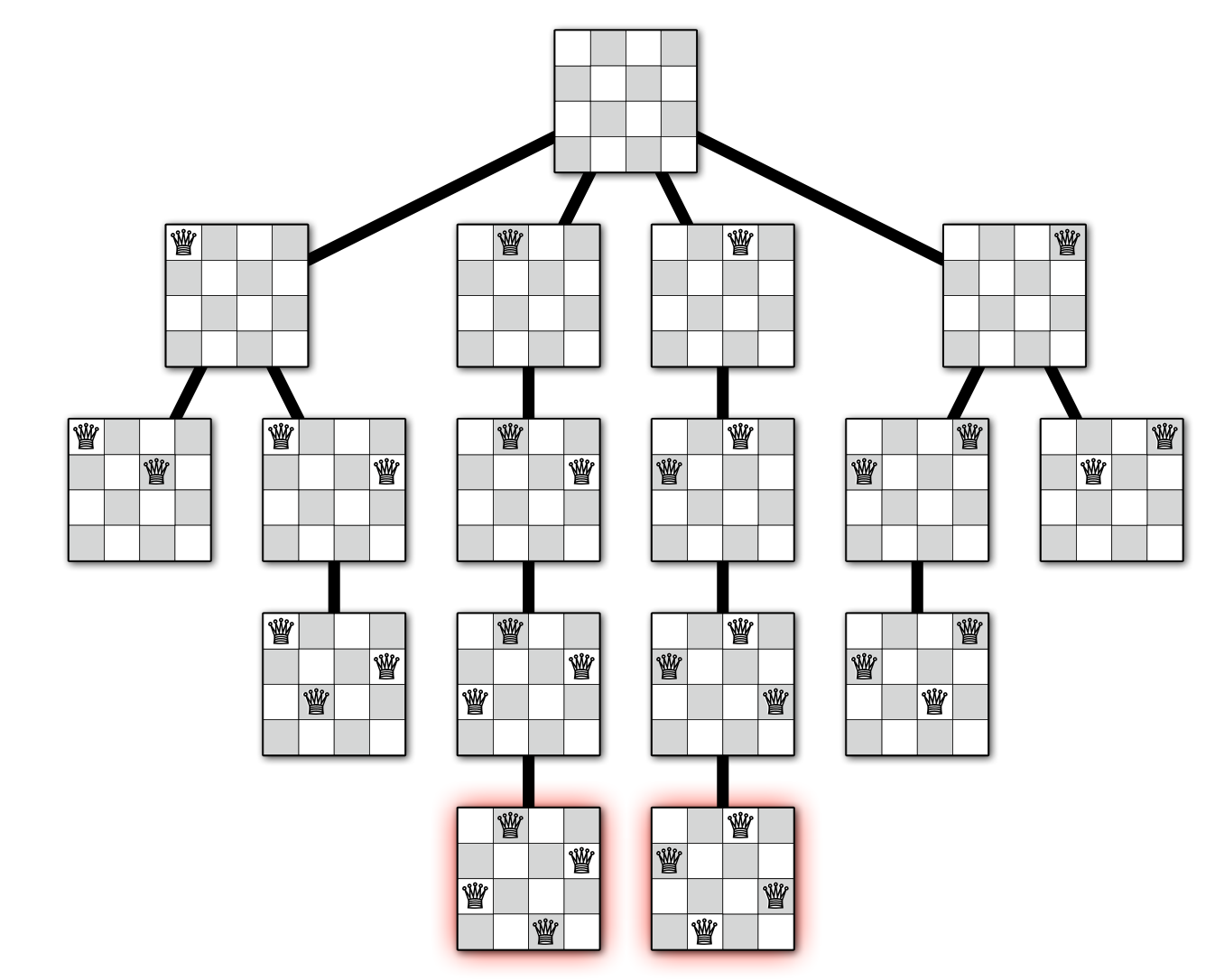
A recursion tree for 4 queens problem

queen을 놓을 수 있는 safe place인지 체크하기 위해서 place(i, j)를 0과 1로 둔다.

0 : safe place

1 : unsafe place

 

is_attack(i, j, board, N):
	//queen 위쪽 직선
    for k in range(1, i):
    	if board[k][j]==1:
        	return TURE		//TRUE로 리턴하는 것은 attack이 가능하다는 것을 의미
	
    //queen 왼쪽 위 대각선
    k=i-1
    l=j-1
    while k>=1 and l>=1:
    	if board[k][l]==1:
        	return TRUE
        k=k-1
        l=l-1
        
    //queen 오른쪽 위 대각선    
	k=i-1
    l=j+1
    while k>=1 and l<=N:
    	if board[k][l]==1:
        	return TRUE
        k=k-1

N-Queen(row, n, N, board):
	if n==0:
    	return TRUE
    for j in range(1, N+1):
    	if not is_attack(row, j, board, N):
        	board[row][j]=1
        	if N-Queen(row+1, n-1, N, board):
            	return TRUE
            board[row][j]=0  //backtracking
	return FALSE

 

*Performance of N-Queen()

N은 고정되어 있고(Queen의 수) n은 문제의 size이다. (남아있는 queen의 수)

N-Queen의 for loop는 1~N까지 run

> is_attack() : O(N) 최대 N번 실행

> recursive call : T(n-1) -> N*O(N) + N*T(n-1)

=> T(N) = O(N^2) + N*T(n-1) = O(n!)