[알고리즘] NP-Completeness(1)

[Computational complexity]

 

알고리즘은 특정 알고리즘의 성능 특성에 대한 연구이다.

 

[The turing machine]

 

- 알고리즘과 계산 개념을 튜링 기계라는 추상 모델을 통해 형식화

- 튜링 머신보다 더 powerful한 디지털 computation 모델은 없다. (추상 기계 중 가장 상위)

 

> Finite automaton : 가장 basic한 추상 기계, read만 가능

q0 : initial state(=start state)

q3 : final state

- input string이 있는 finite tape

- tape는 왼쪽에서 오른쪽으로 read (no going back)

- finite automaton은 추가적 메모리를 가지지 않음

 

> Turing Machine

- 각 arcs에 다른 라벨들

- 추가적인 메모리 많음 (tape)

- tape head (or read-write head)

- 왼/오른쪽으로 이동 가능

- read와 write 모두 가능

- input은 tape에 위치

- tape head : 내가 지금 scan하고 있는 point

1) 맨 처음 tape head는 input들 중 가장 왼쪽에 있는 cell이다.

2) scanned symbol과 finite control의 현재 state이 기반하여 machine이 move

 

*finite automaton은 상태변화만 / turing machine은 3가지 변화

1) state 변화

2) overwrite 여부

3) tape head의 방향(left or right)

 

*튜링 머신에 있는 tape의 각 cell들은..

1) input alphabet(input string을 구성하고 있는 character들의 집합)으로부터의 symbol

2) tape alphabet(tape에 올려놓을 수 있는 모든 character들의 집합)으로부터의 symbol

3) a blank symbol ∆

 

ex) S = 010111 over Σ = {0, 1}

 

***TM is a 7-Tuple

 

EX) δ( q1, b) = (q2, ∆, R)
해석 : 우리는 현재 state q1에 있고, read the cell;it's a b. 그리고 q2로 state를 바꿀 것이며, blank로 write할 것이고, 오른쪽 방향으로 갈 것이다.

1) δ( q0, a) = (q1, ∆, R)

2) δ( q1, b) = (q2, a, L)

=> 이렇게 정의할 수 있어야 함!

 

***해석하기!!!!!!!

 

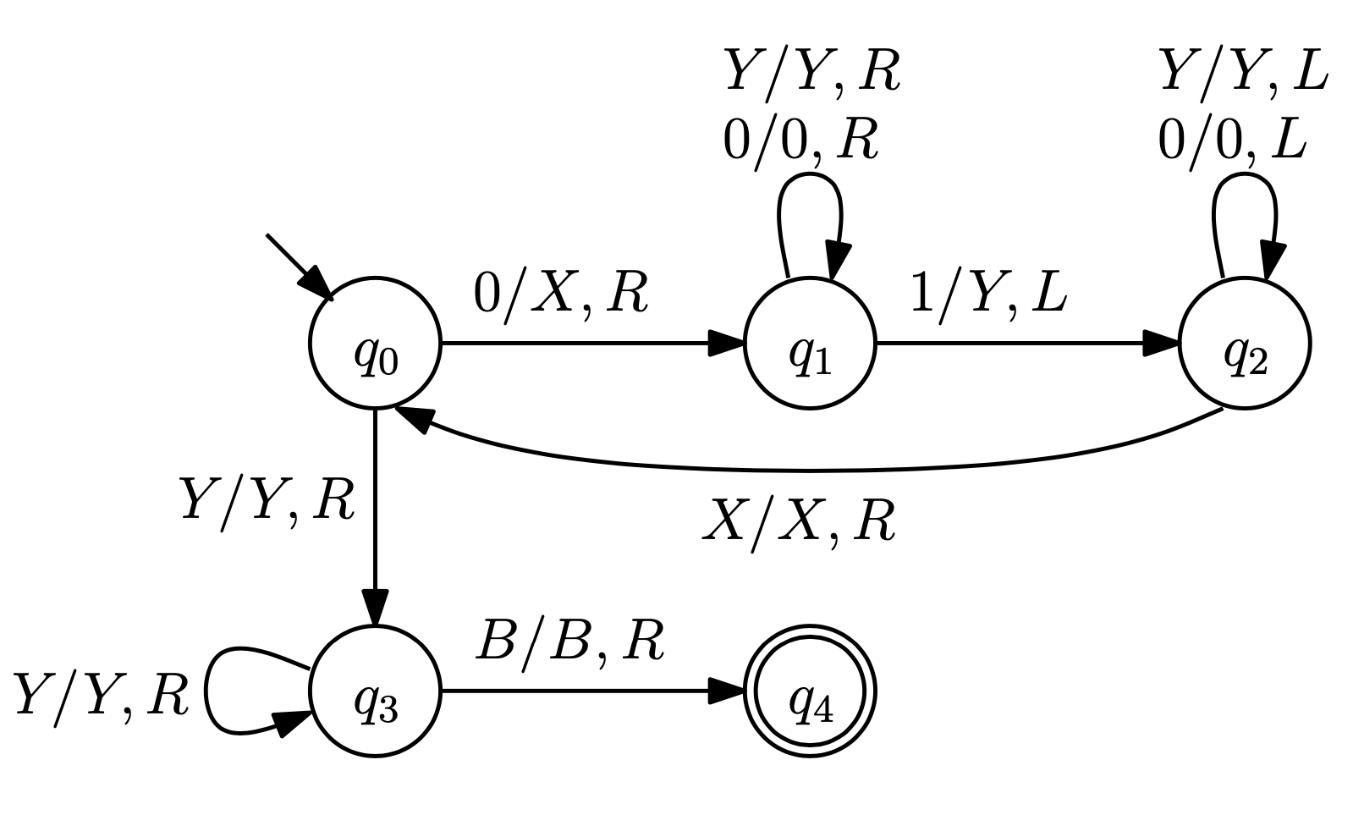
T = (Q, Σ, 𝛤, δ, B, q0, F), where

Q : finite set of states

Σ : input alphabet = {0,1}

𝛤 : tape alphabet = {0, 1, B, Y, X}

B : blank symbol

q0 : start state

F : final state = {q4}

δ : transition function

① δ(q1, Y) = (q1, Y, R)

② δ(q1, 0) = (q1, 0, R)

③ δ(q2, Y) = (q2, Y, L)

④ δ(q2, 0) = (q2, 0, L)

⑤ δ(q1, 1) = (q2, Y, L)

⑥ δ(q0, 1) = (q1, X, R)

⑦ δ(q0, Y) = (q3, Y, R)

⑧ δ(q3, Y) = (q3, Y, R)

⑨ δ(q2, X) = (q0, X, R)

⑩ δ(q3, B) = (q4, B, R)

 

=> input string w(0011)은 TM에 의해 accepted되었다! (if TM이 final state에 도달했을 때만)

 

solvable과 unsolvable 문제로 구분

 

1) Unsolvable problems

2) Solvable problems : 

   a. Provably(입증가능한) intractable (infeasible) problems

   b. Probably intractable problems(아마도 다루기 쉽지 않은)

   c. Tractable problems (feasible problems)

 

 

[Unsolvable Problems]

 

> Crashing and Halting

- state q는 halting for a symbol x∈𝛤 if δ(q, x)가 정의되지 않았을 때

- state q는 halting if it is halting for all symbols in 𝛤

- 우리는 모든 final states들이 halting되는 generality의 손실 없이 가정 가능

 

*2 ways a string fail(accept 못하는 경우)

1) Crashing : transition function이 정의되지 않은 tape에서 symbol이 찾아졌을 때 현재 state가 halt state가 아니라면 we crash

2) Looping : 무한 루프가 발생하는 경우

=> 만약 TM이 crash하면, string은 명백히 rejected된 것!!!!!

=> we can tell that a TM has rejected a string by crashing

=> we cannot tell if a TM has rejected a string by looping indefinitely!

 

> Halting Problem

프로그램 P가 input 데이터를 run(수행)하는 것

두 가지 가능성

1) P halts on i : accept이나 reject이나 결과를 줘서 정확히 halting하는 경우

2) P runs forever on i : 잘못된 데이터로 인하여 무한 루프가 발생하는 경우

 

Question : 프로그램 P와 input i를 읽고 P가 i에서 정지(halt)할지 여부를 결정할 수 있는 프로그램 H가 있는가?

Theorem => The Halting problem is undecidable!

Test(P) :
	if Halt(P, P) == True:
    		return False
	else:
    		return True

Halt(Test,Test)가 Test halts on input Test(True)를 의미한다고 가정하면, 이는 Test(Test) runs foever on input Test를 뜻하게 된다. 

Halt(Test,Test)가 Test runs forever on input Test(False)를 의미한다고 가정하면, 이는 Test(Test) halts on input Test를 뜻하게 된다.

 

=> 두가지는 모두 모순된다. 즉, Halt(P,i)는 존재하지 않는다.

 

EX) 어떤 마을에 스스로 면도하지 못하는 모든 남자만을 면도해주는 남자 이발사가 있다. 이 남자 이발사는 스스로 면도할 수 있을까?

1) 남자 이발사가 스스로 면도할 수 있다면

-> 이 이발사는 스스로 면도하지 못하는 남자만을 면도해주는데, 자기 자신을 면도하면, 면도하지 못하는 남자가 아닌 면도하는 남자인 자신을 면도해주는 것이 된다.

2) 남자 이발사가 스스로 면도할 수 없다면

-> 자기 자신이 스스로 면도하지 못하는 남자의 집합에 속하게 된다. 그러면 이발사 본인은 스스로 면도하지 못하는 남자만을 면도해주므로, 자기 자신을 면도해야 한다.

=> 결국 모순!