[기계학습] Lecture2 - 기계학습을 위한 기초지식

 

*스칼라 : 1, 2, 3.14와 같이 크기 값을 가지는 양

*벡터 : 순서가 있는 스칼라 값의 배열 의미 / 열벡터 표기법 사용

*벡터의 norm : 벡터의 크기

 

[벡터 x의 p차 norm]

p = 1 -> Manhatten distance(차원별 거리의 합)이 되고 l1 norm이라고 한다.

p = 2 -> 유클리디안 norm(벡터의 시작점에서 끝점을 화살표로 표현할 때 화살표의 길이) / l2 norm

 

*벡터 / 유클리드 norm값 = 길이가 1인 벡터(단위벡터;unit vector)

*벡터의 정규화 : 길이 1인 벡터로 만드는 일

 

*Hadamard곱 : 가장 간단하면서도 벡터 연산 여러 영역에서 유용한 곱

*dot product(스칼라곱)

*cross product(벡터곱)

크기와 방향을 갖는 새로운 벡터

 

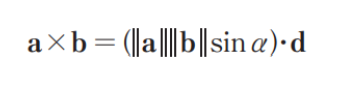
*미분 – 머신러닝에서 사용되는 여러 기법들을 이해하기 위해 필요한 수학적인 개념

미분 : 순간변화량 구하는 것

 

*편미분 : 둘 이상의 변수들을 가지는 함수 f가 있을 경우, 이 함수를 각각의 변수에 대해서 독립적으로 미분을 하는 방식

***편미분을 사용하는 이유 : 다차원 공간에서 정의되는 목적함수의 최적해를 찾기 위해서이다.

 

*머신러닝 : 문제를 해결하는 model(파라미터가 모여진 집합)

*파라미터 : 모델의 동작 결정

*학습(learning) : 파라미터를 더 좋은 상태로 변경하는 것

 

*오차가 없다 = 학습이 완벽하다 = 모델이 데이터를 잘 설명한다

 

*학습 : 오차가 줄어드는 방향(모델이 데이터를 잘 설명하는 방향)으로 파라미터를 변경하는 일

-> 현재 가중치 w 위치에서 오차 곡면의 기울기를 안다면 기울기를 따라 내려가면 곡면을 낮은 곳으로 향할 수 있음

-> 최적해에 도달했다면 기울기 벡터가 0인 벡터가 될 것이며 경사 하강법을 통한 최적화이다.

*지역 최소값(지역 최적값) : 일정한 영역 내에서 가장 좋은 지점

*전역 최소값(전역 최적값) : 전체 공간에서 가장 좋은 해

 

=>경사 하강법을 통한 학습 = 현재의 가중치 w를 더 좋은 가중치 w’로 바꾸는 일

하이퍼파라미터 eta : 기울기의 반대 방향으로 얼마나 이동할 것인지를 결정하는 학습률

 

*과적합 : 머신러닝에서 흔히 발생하는 문제

-> 데이터를 분석한 결과가 특정한 데이터 집합에만 매우 정확하게 일치하고, 다른 데이터에는 잘 들어맞지 않는 상태를 의미

*일반화

학습을 통해 모델의 파라미터를 결정한 뒤에 학습하지 않은 데이터에 모델을 적용하여 값을 예측하거나 분류를 수행하는 등의 데이터 분석을 실시하는 것

***과적합 = 일반화가 제대로 되지 않는다는 것

 

*과적합의 원인

- 학습에 사용된 데이터의 수가 너무 적다는 것

- 데이터를 설명하기 위해 사용된 녹색 곡선이 너무 복잡하다는 것

 

*과소적합 : 학습이 지나치게 덜 이루어져 새로운 데이터뿐만 아니라 학습 데이터조차 제대로 설명하지 못하는 모델

*과소적합 원인

- 모델이 지나치게 단순한 경우 발생

- 예측을 제대로 할 수 없는 특징들만 제공되는 경우에 발생

-> 입력 데이터의 특징을 바꾸거나 학습 모델의 복잡도를 높이는 방법으로 문제 해결

 

*과적합을 피하기 위한 방법

Regularization 기법 : 모델이 복잡하면 불리하게 만드는 복잡성이 발생 -> 복잡해지지 않게 패널티를 적용하는 기법

p : penalty항

-> 학습은 오차를 줄이는 것뿐만 아니라 패널티 항도 같이 줄이는 일을 하게 되고, 이 패널티 항으로 어떤 것을 사용하는가에 따라 regularization의 특성도 달라짐